|
Settings of Quantum Graphs 2
|
|
|
(2.3)
|
If we denote the point on the i-th brach right adjacent to thenode by 0i, and define N-dimensional vectors \Phi and \Phi' by
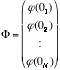 ÅA ÅA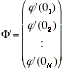 Å@ Å@ |
(2.4)
|
we can easily show, by explicit calculation, that the condition of probability density flus (2.3) is written as
|
|
(2.5)
|
which can be further rewritten as ![]() . Here, L0 is an arbitrary constant with the dimension of length which is introduced to have consistent dimensionality for each term in the equality. This equality signifies the transfomability of the inside of absolute value of LHS to that of RHS by a unitary matrix of dimension N. Writing that unitary matrix belonging to U(N) as U, after some reformulation, we have an equation
. Here, L0 is an arbitrary constant with the dimension of length which is introduced to have consistent dimensionality for each term in the equality. This equality signifies the transfomability of the inside of absolute value of LHS to that of RHS by a unitary matrix of dimension N. Writing that unitary matrix belonging to U(N) as U, after some reformulation, we have an equation
|
|
(2.6)
|
which is the fundamental equation for us. The meaning of L_0, that emmerged from "nowhere" with the dimensional argument will be discussed later in full detail. End result is that the Schroedinger equation (2.2) yields a definite state only when supplemented by the condition (2.6) that specifies how the values of various braches of wave functions are connected at the node x_i=0. The unitary matrix U appearing in that connection condition has N^2 parameters that define the quantum mechanical property of the node. In other word, at the node that is an object of "set of measure zero", there are infitenite number of different quantum point interactions that are specified by N^2 parameters of U(N) matrix.