Quantum Graphs : Physics of Quantum Singularity (2-1)

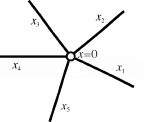
Settings of Quantum Graph 1

Consider a graph made up of many lines crossing each other at various points. In general, we can think of a graph with any desired complications. However, if we cut it into smaller pieces at lines, we will invariably end up with a one with only one node from which many lines are sticking out. We therefore consider one of these elementary graph with one node. Let us assume that there are N lines sticking out, on which we assigne the number i =1, 2, ..., N. We allocate the position at the line i by coordinate xi such that the node is assigned the position of the origine, xi = 0. (See the Figure bellow)

Let us think what will happen if a quantum mechanical particle lives on this graph. If we assume that the particle moves freely on each branch of lines x = x_i of this graph, the motion is described by the free particle Hamiltonian

(2.1)

whose quantum state is described by the stationary Schroedinger equation

(2.2)

Now the problem is the fact that we do not know how the motion is described at the node x_i = 0, which must mean that the node x_i = 0 is a singularity of the hamiltonian operator. We suddenly face a rather fundamental problem whether we can have a legitimate quatum theory of a system whose Hamiltonian is indefinite at one spacial point.

If you go to the library and bring back a random introductory textbook on quantum mechanics, you might see such assertion as "the wave function has to be continuous" without any justification. Assuming that is the case, you face the quation like: what is the meaning of contunuity on multiply connected node? What about the continuity of derivatives of wave function? Surely, you remenber that famous Dirac delta function potential whose solution has discontinuity in the derivative of wave function. Obviously, we need to go back to the very basic of quantum mechanics