Quantum Graphs : Physics of Quantum Singularity (3-2)

Geometry of Parameter Space 2

Let us now assume that the matrix U is diagonalized by a unitary transformation and the resulting diagonal matrix is D given by

(3.4)

Here, the angles \theta_+ and \theta_- are with the rage [0, 2\pi). We consider an element of SU(2) group as V, which we explicitely write as . The Euler angles , using Euler angles \mu and \nu take real number within the range [0, π] and [0, 2\pi) . Explicit calculation shows that the matrix U is expressible, in terms of a "spin" matrix

(3.5)

as

(3.6)

Namely, U is split into a diagonal matrix and spin roation. Because the spin matrix \sigma_V has the property , previous argument indicates that (3.6) shows the spectral equivalence of U and D. Since D is fully determined by two parameters that specify the eigenvalues of U, we can conculde that the spectrum of U is uniquely decided by its eigenspectra.

Expression (3.6) also suggests that the U(2) matrix U has a natural representation with four parameters two of which are eigen angles (\theta_+, \theta_-) and another two (\mu, \nu). Consiering their range and functions, we can conclude that the manifold S_4 that represents the entire parameter space of quantum point interaction can be thought of as spittable into the spectra-deciding torus T² = {(\theta_+, \theta_-)} , and equispectral sphare S² = {(\mu, \nu)} . (See Figure 3 bellow)

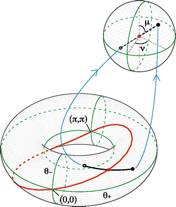Fig. 3