Quantum Graphs : Physics of Quantum Singularity (4-2)

Two Examples 2

The most general parity invariant point interaction is specified by (\theta_+, \theta_-) without any constraint on either value. We can view it as the coexistent state of delta and epsilon (delta-prime) potentials., each acting only on symmetric and antisymmetric components of the state wave function. For overview of the whole family of interactions, we have drawn a disected version of the torus representing the parameter space of the parity invariant point interactions in Fig. 4. On this figure, left and right edges represent the same interactions, so are the top and bottom edges. The red solid line, \theta_- = \pi corresponds to the delta [potential and the blue dashed line, \theta_+ = 0, the epsilon potential.

Symmeric eigenstates of a system is determined solely by the parameter \theta_+ and not affected by the value of \theta_- at all. Similarly, the antisymmetric states are determined solely by \theta_- and no effect will be observed on them by the variation of \theta_+. Therefore, any point on this square (torus) can be parallel-transported perpendicularly onto the blue dashed line, the epsilon potential, with its antisymmetric spectra intact, while it is horizontally parallel-transportable onto the red solid line, the delta potential, with its symmetric spectra intact. This is the precise meaning of any parity conserving point interaction being the combination of delta and epsilon.

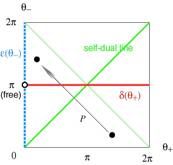
Fig.4 Disection of P_1 invariant (parity invariant) torus

Consider a transformation P on this square (black arrow) that mirror-reflects all point by the green diagonal line \theta_+ = \theta_-. This P is called "dual transformation", and two points connected by P are termed "dual" to each other. P = P_2 or P=P_3 (or any unimodular linear combination) will just do. As explained before, P keeps the entire spectra of a system intact after the mapping, but it is done by replacing every symmetric state by a corresponding antisymmetric state. Therefore, upper-left and lower-right triangles separated by the green diagonal line are spectrally equivalent. The other way of stating is that spectrally distict ones among entire poin interactions are fully enumerated by just considering "half of torus", either one of these two triangles.

Remarkable locations on this torus is the green diagonal itself where we have \theta_+ = \theta_-. On this line, we have

(4.6)

and the system is "self-dual" and mapped onto itself by the duality transformation. This means that the transformation P_2 will leave the spectra of system unchanged while exchanging entire symmetric states with antisymmetric states. The only way this can happen is by having equispectral pairs of symmetric and antisymmetric states. Namely, along the diagonal line, the system is doubly degenerate with symmetric and antisymmetric states for every eigenvalue, apart from the ground state which forms an exception. Clearly, this is an example of the super symmetry