|
パラメタ空間の幾何学2
|
|
|
(3.4)
|
とかく。ここで は [0, 2π) の範囲の角度変数である。SU(2) の要素 V をオイラー角 (μ, ν) を用いて ![]() と書いてみる。ここで μ、ν はそれぞれ [0, π]、 [0, 2π) の範囲の実数である。直接の計算によって容易に示せるようにU は次の行列
と書いてみる。ここで μ、ν はそれぞれ [0, π]、 [0, 2π) の範囲の実数である。直接の計算によって容易に示せるようにU は次の行列
|
|
(3.5)
|
をもちいて
|
|
(3.6)
|
とも書ける。つまり行列 U を対角行列とスピン回転に分解できたわけである。スピン行列 σV は の性質を持つから( に注意)先ほどの議論を適用するとUとDは同じスペクトルを持つ事が分る。これを言い変えると、Uのスペクトルはその固有値によって一意的に決まるという結論が得られる[6]。
表現(3.6)はまた、Uの「自然なパラメタ」として固有角 (θ+, θ-) とオイラー回転角 (μ, ν) の四つを与えている。つまり点状相互作用全体をあらわすパラメタ空間である多様体 S4 はスペクトルを決めるトーラス T2 = {(θ+, θ-)} と等スペクトル変換の集合をあらわす球面 S2 = {(μ, ν)} に分けて考えることができる(図3)。
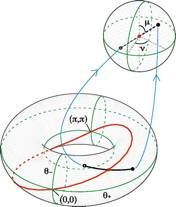 図3 |