Design of controllable single electron elements to contribute to the practical implementation of quantum computers

LANGUAGE ≫ Japanese

ZEN, Takuju

Specialized field: Theoretical Physics, Quantum Engineering, Sociophysics

For Details

A desire to explore the mysteries of quantum mechanics and put them to work in advanced technology

A quantum is a tiny unit of matter or energy with the properties of both particles (matter) and waves (states). In this extremely small, special world, the physical laws of ordinary life no longer hold. Instead, events follow a mysterious set of laws called quantum mechanics.

　It's been more than 100 years since quantum mechanics was first discovered, and even today, its full picture is wrapped in mystery. Professor Zen says that "The more seriously we think about quantum theory, the harder it is to reconcile with common sense." He has used mathematics to investigate the mysterious and beautiful behavior of quanta, and conducted research to extract its essence in a tangible form, so it can be put to use in technology.

Probabilistic determination of events exemplifies the mystery of quanta, with different results occurring even in the exact same situation.

"If, for example, force is applied to an electron, the states of going to the right and the left exist simultaneously, and the probability is 50% each way. It's like the mind of a person, always vacillating. The electron simultaneously has two conflicting states, as if it had a mind of its own."

Quantum mechanics is the foundation of some of today's most advanced technologies, such as lasers and semiconductors, and in recent years quantum computers have raised expectations as a potential new application. Quantum computers are said to have 100,000 times the processing power of conventional computers, and they make use of the peculiar quantum property whereby two states can exist simultaneously.

　In a conventional computer, data is processed as combinations of 1s and 0s, and it's impossible to simultaneously represent two or more states. A quantum computer, on the other hand, can represent two or more states simultaneously. This makes it possible to carry out multiple calculations in parallel, and problems with many alternatives like prime factorization can be solved at high speed. In October 2019, a demonstration of quantum supremacy was reported by a research team at Google, and quantum computers are once again garnering attention.

"The idea of quantum computation has been around for about 30 years. At first, it was just a mathematical theory, but today it is becoming a real, important presence, and it's amazing that quanta have become a topic of conversation all over the world. Strange properties that violate common sense exist, even in the real world, and it's fascinating that this technology has taken shape and become a reality in the 100 years since the discovery of quantum mechanics."

Devising new elements based on quantum graph theory to exploit mysterious quantum properties

Although technical innovation is making progress, current quantum computers must be kept at ultra-low temperatures close to absolute zero, so practical application is still a long way away. Working with Dr. Pavel Exner (Doppler Institute, Czech Technical University) one of the leading mathematical physicists in Europe, Professor Zen is conducting research on "quantum graph theory." This topic is attracting attention as a theoretical model for single electron devices, and may help develop next-generation single electron elements for practical implementation of quantum computers. Quantum graph theory examines how to control the movement of quantum particles (electrons) in circuits composed of ultra-fine wires on the nanometer level.

"As many as 1 million electrons flow through each transistor in a computer. This is actually a tremendous waste at the atomic level. To enable use of quantum computers at ordinary temperatures, we will need to minimize the number of electrons flowing through the circuitry, and the ultimate aim is transistors where only one electron passes through complexly laid out wires. Investigating methods of controlling such single electrons is the task of quantum graph theory."

Technology for controlling the motion of single electrons is making progress, and recent years have seen growing expectations on quantum graph theory as a framework for theoretically handling these issues. "Quantum graphs have been closely investigated for a long time due to their mathematical interest, but now they are regarded as a model of quantum single electron elements at the nanoscale," he says, with some excitement.

　Professor Zen says the mystery of quantum mechanics is especially prominent when handling quantum particles that move through a graph made of points and lines. For example, consider a particle moving along a straight line that runs into a point. In classical mechanics, the particle can only bounce back or pass through. In quantum mechanics, however, the particle is a probability wave, so it can partially pass through, and, depending on the energy of collision, it may sometimes pass through and sometimes not. It may also pass through if it strikes gently, and bounce back if it strikes forcefully.

　Professor Zen and his colleagues have designed various systems using virtual techniques, and analyzed all of the phenomena which occur at nodes where lines overlap. The results have shown that strange phenomena--not seen in ordinary quantum mechanics--occur at the nodes of a quantum graph. It was also found that if multiple nodes exhibiting simple responses are concentrated in a region smaller than the wavelength of the quantum wave, they behave as "integrated quantum nodes" that operate cooperatively and exhibit unusual response. In this way, Professor Zen et al. have elucidated the mathematical properties of nodes in quantum graphs, and developed a theory of their applications.

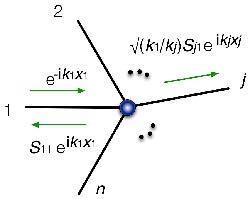
(Scattering of quantum particles on a graph)

" We have shown how to control nodes in quantum graphs, and how nodes can be used to control electrons. We have, loosely speaking, done the basic design for a single electron element."

　As a spectral filter using a quantum graph, Professor Zen and his colleagues have also devised a model that can be controlled by applying voltage from the outside. Eventually, they believe it will be possible to use this approach in quantum transistors which control the movement of individual electrons. If such devices are realized, they will have ultra-high-speed, lower voltage, and far higher efficiency than conventional electronic circuits. Professor Zen and his colleagues have opened up a new path to controllable quantum spectral filters.

　Going forward, they will continue their theoretical investigations, and strive to create and experimentally verify quantum nano structures by using the "mist CVD method." This method, developed by Professor Toshiyuki Kawaharamura of Kochi University of Technology and his colleagues, enables deposition of large-area, high-quality functional thin films at atmospheric pressure. R&D on new quantum elements based on quantum graph theory will likely lead to development of advanced, next-generation functional devices.

"If something exists theoretically, it should definitely be feasible. There are only a handful of laboratories dealing with quantum graph theory in the world, but if our results are demonstrated experimentally, more researchers will get involved, and the field will be globally energized. I firmly believe practical implementation will be in progress 20 years from now."

The opinion of the majority does not always win out. Clarifying the realities of majority rule democracy

While pursuing the mysterious behavior of quanta, Professor Zen is also engaged in research on social physics--a discipline which investigates human behavior and social phenomena using the perspectives and techniques of physics. One particular theme he is working on is "how the wills of individuals are aggregated, and connected with decision-making of each group as a whole."

　Are there mathematical laws describing how majority opinions are formed? When people with free will form a majority, is the governing law similar to how numerous atoms aggregate into a material substance? Opinion dynamics is a field which arose from such ideas, and it models the formation of majorities in social groups within the framework of mathematical physics. Working with Serge Galam (Paris Institute of Political Studies), a theoretical physicist regarded as the father of opinion dynamics, Professor Zen has conducted research to help further develop the field.

　Majority decisions--used in all areas of decision-making--are mathematically justified based on the principle that "two heads are better than one." That is, if a majority decision is taken by gathering people whose decision certainty is 50% or greater, then as the number of people increases, a decision certainty close to 100% is obtained. However, the reality of democratic elections deviates from that assumption. Many people with no insight on a given issue can't make a good decision even if they think about it, and people are also easily influenced by the opinion of others. Therefore, it's common for many people's opinions to simply imitate other people. As a result, it often happens that decisions by minorities with strong opinions quickly spread to a majority.

　For example, suppose that two headache medications are being sold on the Internet: A with an ingredient whose efficacy has been pharmacologically demonstrated, and B which has no active ingredient. The seller of B, a placebo, has strong advertising capabilities, and agents of the seller pose as buyers, leaving comments on an e-commerce site promoting B and criticizing A. Meanwhile, the seller of A, which is actually effective, does almost no advertising.

　In this situation, the question of whether A or B will sell is determined by how much insight the buyers have about drugs. If the people who visit the site to buy drugs are nonprofessionals with no medical knowledge, they will read a few of the written reviews and likely buy B. Conversely, if the people who visit the site are healthcare professionals, they are likely to compare the lists of ingredients in the two drugs and buy A without hesitation.

　Now, what happens in the intermediate case? Professor Zen and his colleagues concluded that if the percentage of professionals with insight is a little less than 20% of the group or higher, the effective drug will sell, and conversely, if the percentage of professionals with insight is a little less than 20% or lower, then the drug with no efficacy and strong advertising will sell. This conclusion has already been demonstrated experimentally by other researchers.

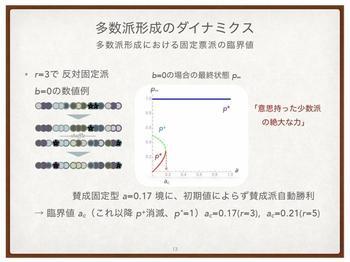
"For example, if people with a certain strong opinion make up a little less than 20% of a group or more, then they will win out over the remaining people, even though the percentage with a strong opinion is small. Even in a democracy, the opinion of the majority does not always carry the day. The opinion of a minority such as an interest group may be more influential.".

The new model of majority formation in social groups discovered by Professor Zen and his colleagues reveals the truth of majority rule democracy, i.e., the difference between ideals and reality.

"We discovered this instructive result by using a spin model from physics, simplifying the opinions of individuals, and treating them like electrons. There are many kinds of people in the world, so we will pursue this research further--assuming various scenarios, like what happens if there are headstrong people mixed in, like the people of Kochi, who oppose the people with strong opinions."

　Due to the development of fields like artificial intelligence, the trend of incorporating mathematics and physics into the fields of social science will likely progress further in the future. The results of Professor Zen and his colleagues will help lead the way in research analyzing society with mathematical and physical techniques.

"If people who spread misinformation are mixed in at a rate of a little less than 20% or more, many people will be deceived. If we publicize this fact, people will protect their beliefs with a safety buffer, and not immediately and gullibly believe things they see on the Internet. This will make it more difficult to maliciously manipulate information. Our theory, found through collaborative research, is likely to be used in practice in the near future."

The ability to take up new themes, and not be boxed in by received ideas. Freedom is the attraction of physics

At one time, Professor Zen thought of becoming an architect because he wanted to create beautiful order in the world. What is the appeal of physics over architecture?

"Physics is more abstract than architecture, so it offers greater freedom. You can treat human beings using theoretical ideas and mathematical techniques, and you can try out wild ideas. Freedom is the greatest appeal. It's enjoyable to not be held back by rigid thinking, to clear away frameworks, and think hard about strange things that most people don't think about. The people of Kochi are free thinkers, and shy away from constrained "group think." That straightforward approach is a great way to think about physics."

From his base in Kochi, Professor Zen conducts international research with researchers all over the world. The free, big-hearted milieu of Kochi, and the temperament of its people, seem to have had a marked effect on his own research.