Graph Basics with PyPlot

• First, import

                  using PyPlot
                  rc("font", family = "MS Gothic")
                

• Graph Basics

                  # Securing the drawing area
                  fig = figure() 
  
                  # Securing axes
                  # If there is only one graph, 1,1,1 is fine.
                  # This number changes when multiple graphs are arranged side by side, but this will be explained later.
                  ax = fig.add_subplot(1,1,1)
  
                  # Draw a line graph on the axis
                  # Line graphs are plot, and scatter plots (without lines) are scatter
                  # However, you can also draw scatter plots using plot
                  ax.plot([1;4;7], [2;5;1]) # Line graph connecting (1,2),(4,5), and (7,1)
  
                  # graph drawing
                  show()
                  # The following line is also required for drawing in VS Code (not required for Jupyter notebook).
                  PyPlot.display_figs()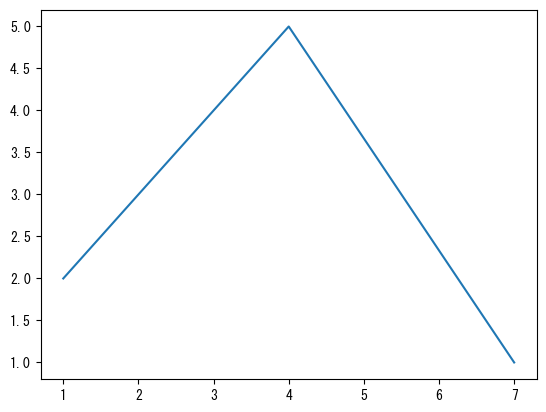
                

  

• mark with a dot (point)

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
  
                  # You can draw points at coordinates specified with the marker option
                  # marker = "o" : round dot
                  # marker = "x" : cross mark
                  # marker = "^" : triangles
                  ax.plot([1;4;7], [2;5;1], marker = "o")
  
                  show()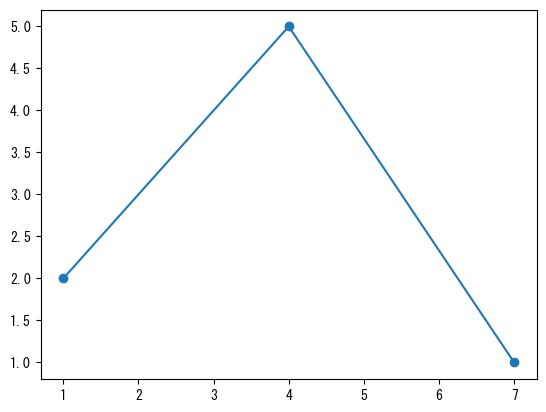
                

  

• Change line type

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # Line style can be changed with the linestyle option
                  # linestyle = "dashed"
                  # linestyle = "dotted"
                  # linestyle = "dashdot"
                  # linestyle = "none" : No line (can be used with markers to create a scatter plot)
                  ax.plot(x, sin.(x), linestyle = "dashed")
  
                  show()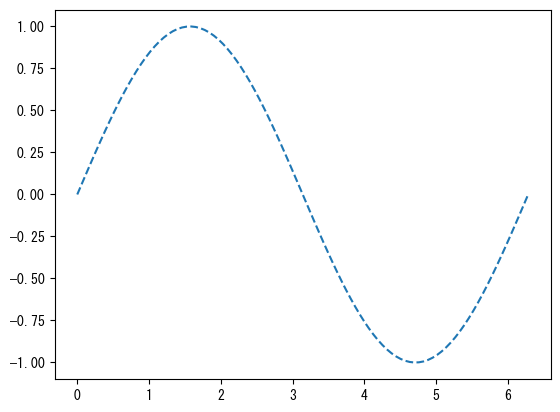
                

  

• Change the color

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # # You can change the color using the color option (the color of the dots will also change at the same time)
                  # color = "red"
                  # color = "tab:red"
                  # color = "black"
                  ax.plot(x, sin.(x), color = "tab:green")
  
                  show()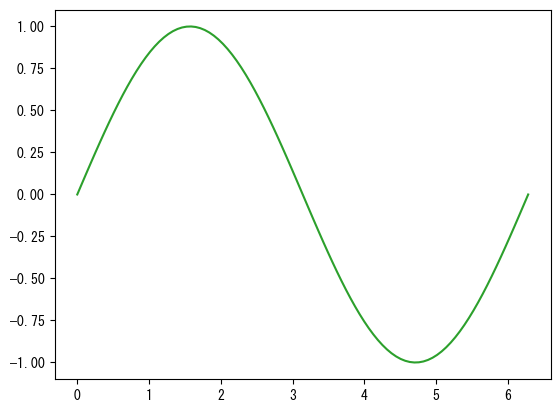
                

  

• Name the axis

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # ax.set_xlabel assigns a name to the x-axis
                  ax.set_xlabel("name of x-axis")
                  # ax.set_ylabel assigns a name to the y-axis
                  ax.set_ylabel("name of y-axis")
  
                  ax.plot(x, sin.(x))
  
                  show()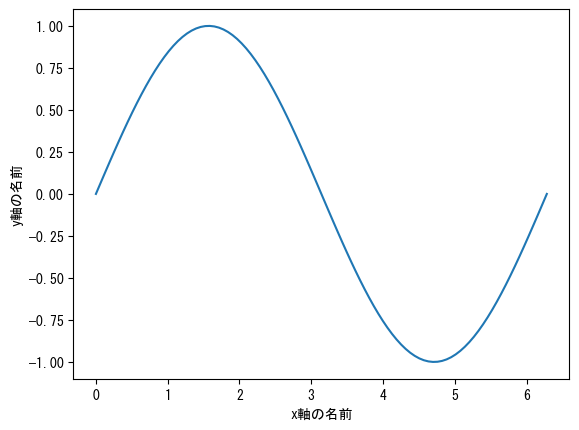
                

  

• Name the graph

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # ax.set_title gives the graph a name
                  ax.set_title("graph of sin(x)")
  
                  ax.plot(x, sin.(x))
  
                  show()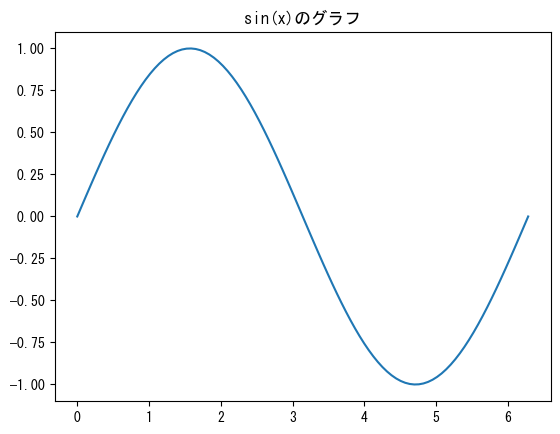
                

  

• Set the axis range

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # You can change the range of the x-axis with ax.set_xlim
                  ax.set_xlim(0, pi)
                  # You can change the range of the y-axis with ax.set_ylim
                  ax.set_ylim(-5, 5)
  
                  ax.plot(x, tan.(x))
  
                  show()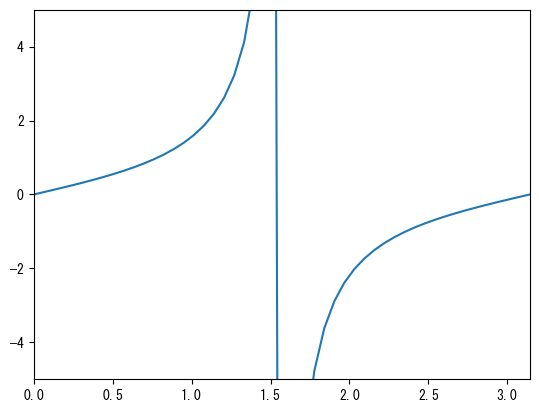
                

  

• Set axis values

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # ax.set_xticks (vector) allows you to display only the desired parts of the x-axis values
                  ax.set_xticks(np.array([0, np.pi/2, np.pi, 3*np.pi/2, 2*np.pi]))
                  # ax.set_yticks (vector) allows you to display only the desired parts of the y-axis values
                  ax.set_yticks(np.array([-1, -0.5, 0, 0.5, 1]))
  
                  ax.plot(x, sin.(x))
  
                  show()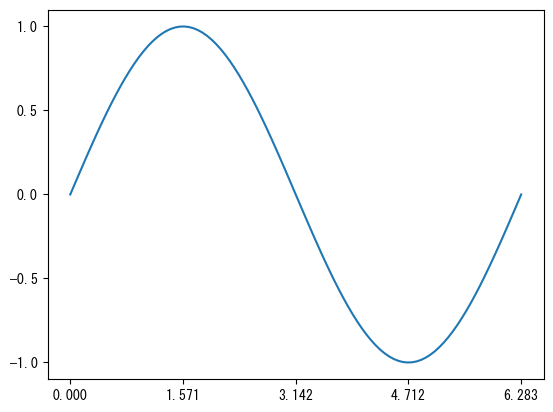
                

  

• Set the values of the axes to whatever notation you want

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  ax.set_xticks([0; pi/2; pi; 3pi/2; 2pi])
                  # ax.set_xticklabels (vector) allows you to change the display of the values set with xticks
                  # The number of elements in the vectors ax.set_xticks and ax.set_xtickslabels must be the same
                  ax.set_xticklabels(["0"; "π/2"; "π"; "3π/2"; "2π"])
  
                  ax.set_yticks([-1; 0; 1])
                  # ax.set_yticklabels (vector) allows you to change the display of the values set with yticks
                  # The number of elements in the vectors ax.set_yticks and ax.set_ytickslabels must be the same
                  ax.set_yticklabels(["ymin"; "0"; "ymax"])
  
                  ax.plot(x, sin.(x))
  
                  show()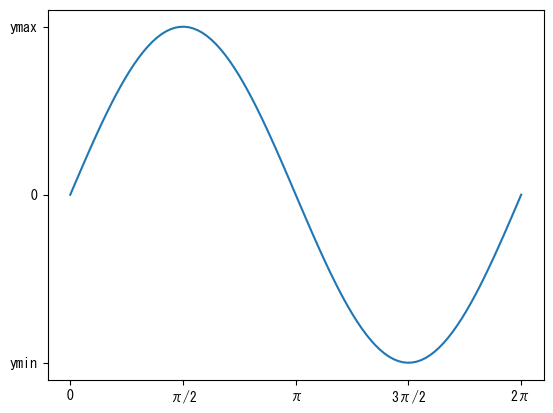
                

  

• Grid against the scale

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  ax.set_xticks([0; pi/2; pi; 3pi/2; 2pi])
                  ax.set_xticklabels(["0"; "π/2"; "π"; "3π/2"; "2π"])
                  # ax.set_grid (axis = "x") adds a grid to the x-axis tick marks
                  ax.grid(axis = "x")
  
                  ax.set_yticks([-1; 0; 1])
                  ax.set_yticklabels(["ymin"; "0"; "ymax"])
                  # ax.set_grid (axis = "y") adds a grid to the y-axis tick marks
                  ax.grid(axis = "y", color="tab:red", linestyle = "dashed")
  
                  ax.plot(x, sin.(x))
  
                  show()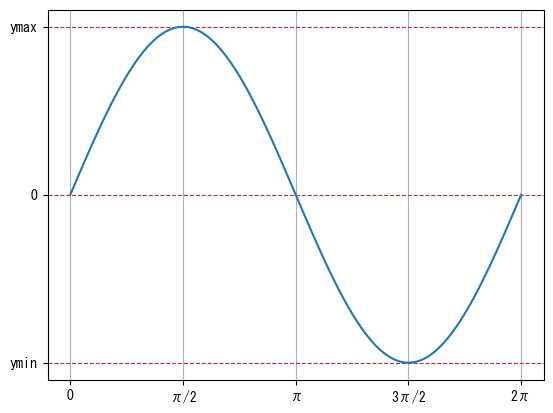
                

  

• Attach a small scale with no numerical value

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  ax.set_xticks([0; pi/2; pi; 3pi/2; 2pi])
                  ax.set_xticklabels(["0"; "π/2"; "π"; "3π/2"; "2π"])
                  # minor = true option sets the minor tick mark setting
                  ax.set_xticks([pi/4; 3pi/4; 5pi/4; 7pi/4], minor = true)
  
                  ax.set_yticks([-1; 0; 1])
                  ax.set_yticklabels(["ymin"; "0"; "ymax"])
  
                  ax.plot(x, sin.(x))
  
                  show()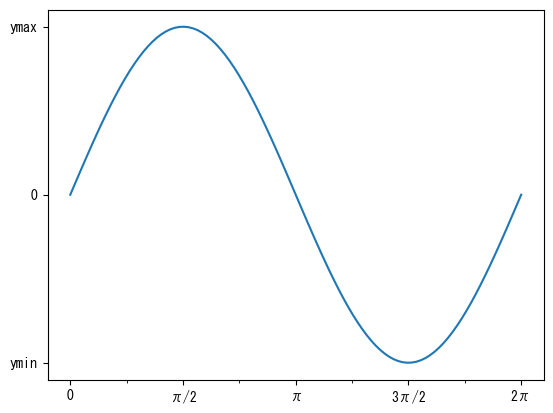
                

  

• Attach grid to small scale

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  ax.set_xticks([0; pi/2; pi; 3pi/2; 2pi])
                  ax.set_xticklabels(["0"; "π/2"; "π"; "3π/2"; "2π"])
                  ax.set_xticks([pi/4; 3pi/4; 5pi/4; 7pi/4], minor = true)
                  ax.grid(axis = "x")
                  # which = "minor" option makes the grid for minor tick marks
                  ax.grid(axis = "x", which = "minor", linestyle = "dashed")
  
                  ax.set_yticks([-1; 0; 1])
                  ax.set_yticklabels(["ymin"; "0"; "ymax"])
  
                  ax.plot(x, sin.(x))
  
                  show()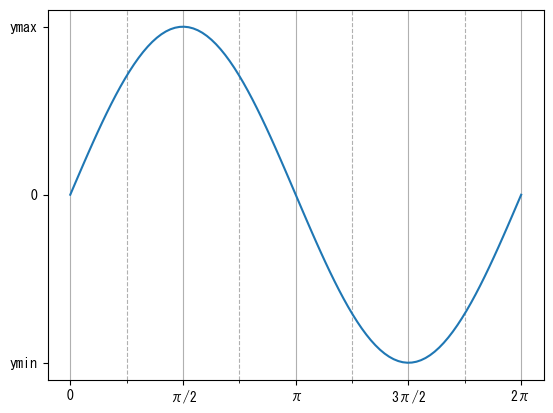
                

  

• Same ratio of length to number on x-axis and y-axis

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # ax.set_aspect(1) sets the ratio of the vertical and horizontal values to be the same
                  ax.set_aspect(1)
  
                  ax.plot(x, sin.(x))
  
                  show()
                

  

• Using LaTeX for Strings

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # By adding an L before a string, you can use LaTeX notation
                  # ax.set_x(y)label, ax.set_title, ax.set_x(y)ticklabels, label (described later) etc. correspond to this
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$\sin(x)$")
                  ax.set_title(L"graph of $\sin(x)$")
  
                  ax.set_xticks([0; pi/2; pi; 3pi/2; 2pi])
                  ax.set_xticklabels(["0"; L"$\pi/2$"; L"$\pi$"; L"$3\pi/2$"; L"$2\pi$"])
  
                  ax.set_yticks([-1; 0; 1])
                  ax.set_yticklabels([L"$y_\mathrm{min}$"; "0"; L"$y_\mathrm{max}$"])
  
                  ax.plot(x, sin.(x))
  
                  show()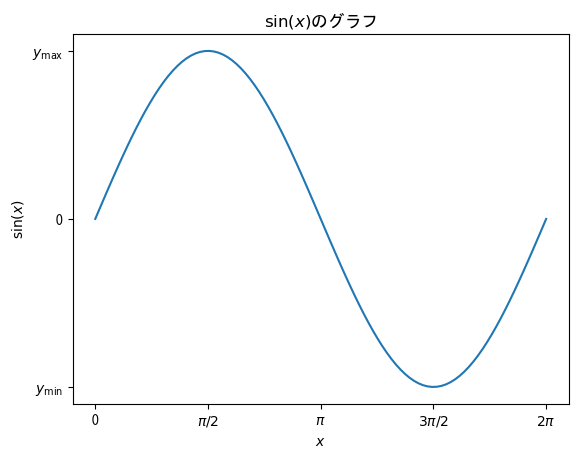
                

  

• Graph size

                  # You can change the size of the drawing area with the # figsize option
                  # The default is [6.4; 4.8]
                  fig = figure(figsize = [6.4; 4.8] * 0.75) 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
                  ax.plot(x, sin.(x))
  
                  show()
                

  

• Saving Graphs

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
                  ax.plot(x, sin.(x))
  
                  # Instead of show(), use savefig("filename") to save the graph
                  # By setting bbox_inches = "tight" and pad_inches = 0.1 as options, you can minimize the extra space around the image
                  # Commonly used file extensions include png and pdf (the file type is automatically determined based on the file extension)
                  savefig("graph.png", bbox_inches = "tight", pad_inches = 0.1)
                

Multiple Graphs

• Draw multiple graphs on a single axis

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # By repeatedly using ax.plot and ax.scatter, you can draw multiple graphs on a single axis
                  # The color changes automatically (of course, you can specify each color individually with the color option)
                  ax.plot(x, sin.(x))
                  ax.plot(x, cos.(x))
  
                  show()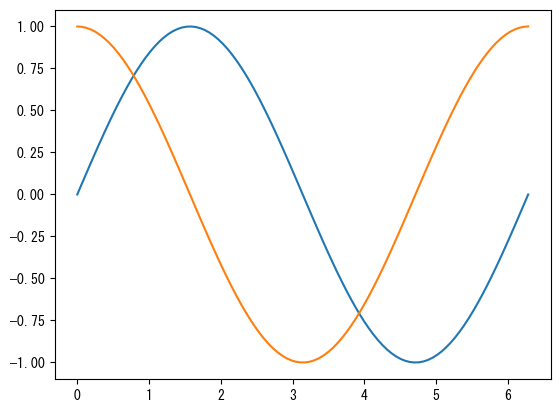
                

  

• Mixed plot and scatter

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x1 = collect(range(0, 2pi, length = 100))
                  x2 = collect(range(0, 2pi, length = 10))
  
                  # You can also mix ax.plot and ax.scatter
                  # Note that color management is separate for plot and scatter
                  ax.plot(x1, sin.(x1))
                  ax.scatter(x2, cos.(x2))
  
                  show()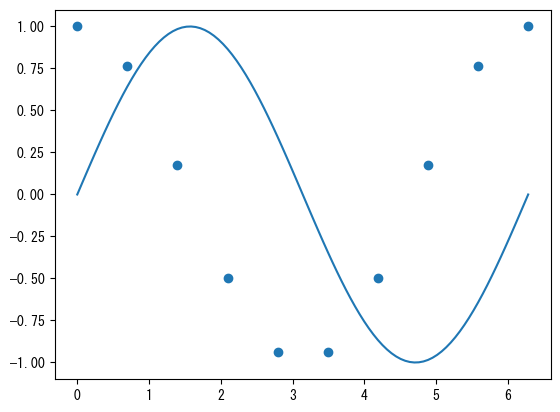
                

  

• Show legend

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  # Name with the label option
                  ax.plot(x, sin.(x), label = L"$\sin(x)$")
                  ax.plot(x, cos.(x), label = L"$\cos(x)$")
  
                  # With ax.legend(), you can display the names assigned with the label option as a legend
                  ax.legend()
  
                  show()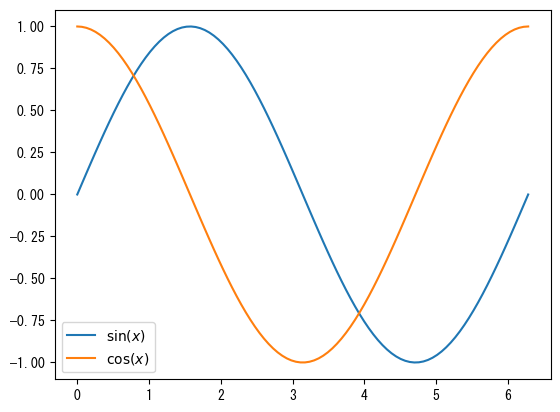
                

  

• Legend Location

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  ax.plot(x, sin.(x), label = L"$\sin(x)$")
                  ax.plot(x, sin.(x .- 2pi / 5), label = L"$\sin(x-2\pi/5)$")
                  ax.plot(x, sin.(x .- 4pi / 5), label = L"$\sin(x-4\pi/5)$")
                  ax.plot(x, sin.(x .- 6pi / 5), label = L"$\sin(x-6\pi/5)$")
                  ax.plot(x, sin.(x .- 8pi / 5), label = L"$\sin(x-8\pi/5)$")
  
                  # The position of the legend is adjusted automatically, but you can specify the approximate position using loc
                  # "upper left"
                  # "upper center"
                  # "upper right"
                  # "center left"
                  # "center"
                  # "center right"
                  # "lower left"
                  # "lower center"
                  # "lower right"
                  ax.legend(loc = "center")
  
                  show()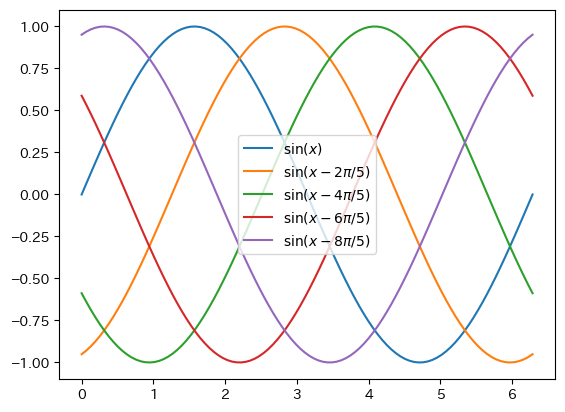
                

  

• Detailed location of legend

                  fig = figure() 
                  ax = fig.add_subplot(1,1,1)
                  x = collect(range(0, 2pi, length = 100))
  
                  ax.plot(x, sin.(x), label = L"$\sin(x)$")
                  ax.plot(x, sin.(x .- 2pi / 5), label = L"$\sin(x-2\pi/5)$")
                  ax.plot(x, sin.(x .- 4pi / 5), label = L"$\sin(x-4\pi/5)$")
                  ax.plot(x, sin.(x .- 6pi / 5), label = L"$\sin(x-6\pi/5)$")
                  ax.plot(x, sin.(x .- 8pi / 5), label = L"$\sin(x-8\pi/5)$")
  
                  # You can specify the position with bbox_to_anchor. (0,0) is the lower left corner, (1,1) is the upper right corner
                  # Furthermore, by specifying loc, you can set the position of the legend to bbox_to_anchor
                  # Specify the number of columns with ncols
  
                  ax.legend(bbox_to_anchor = (0.5, 1), loc = "lower center", ncols = 5)
  
                  show()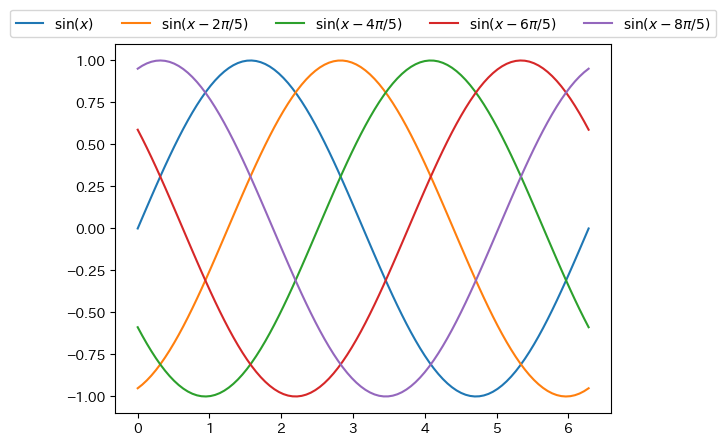
                

  

• Different y-axis for left and right

                  fig = figure() 
                  t = collect(range(0, 0.9, length = 100))
  
                  # First, create a graph for the left side (normal) of the y-axis
                  ax1 = fig.add_subplot(1,1,1)
  
                  ax1.plot(t, 5 .- 9.8 * t)
                  ax1.set_xlabel("time [s]")
                  ax1.set_ylabel("velocity [m/s]")
  
                  # Create a graph for the y-axis on the right side
                  # Creating an axis with the y-axis on the right using twinx
                  ax2 = ax1.twinx()
  
                  # Please note that color management is separate for ax1 and ax2
                  ax2.plot(t, - 4.9 * t .^ 2 + 5 * t)
                  ax2.set_ylabel("height [m]")
  
                  show()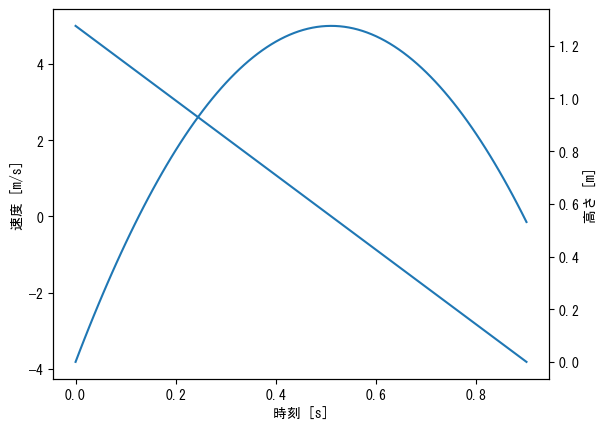
                

  

• Different y-axis for left and right (color, legend adjustment)

                  fig = figure() 
                  t = collect(range(0, 0.9, length = 100))
  
                  ax1 = fig.add_subplot(1,1,1)
  
                  ax1.plot(t, 5 .- 9.8 * t, label = "velocity (without friction) ")
                  ax1.plot(t, 24.6 * exp.(- t / 2) .- 19.6, label = "velocity (with friction) ")
                  ax1.set_xlabel("時刻 [s]")
                  ax1.set_ylabel("velocity [m/s]")
                  ax1.legend()
  
                  ax2 = ax1.twinx()
  
                  ax2.plot(t, - 4.9 * t .^ 2 + 5 * t, label = "height (without friction) ", color = "tab:green")
                  ax2.plot(t, 49.2 * (1 .- exp.(- t / 2)) - 19.6 * t, label = "height (with friction) ", color = "tab:red")
                  ax2.set_ylabel("height [m]")
                  ax2.legend()
  
                  show()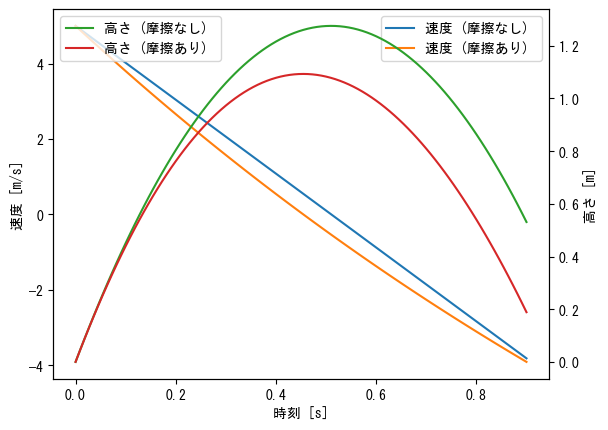
                

  

• Multiple axes

                  # Be sure to set the size of the drawing area, as multiple axes will be drawn
                  fig = figure(figsize = [6.4 * 2; 4.8 * 3] * 0.8) 
                  x1 = collect(range(- pi, pi, length = 100))
                  x2 = collect(range(-1, 1, length = 100))
                  x3 = collect(range(-2, 2, length = 100))
                  x4 = collect(range(1, 2, length = 100))
  
                  # The first one when the axes are arranged in three rows and two columns
                  ax = fig.add_subplot(3,2,1)
                  ax.plot(x1, sin.(x1), label = L"$\sin(x)$")
                  ax.plot(x1, cos.(x1), label = L"$\cos(x)$")
                  ax.plot(x1, tan.(x1), label = L"$\tan(x)$")
                  ax.set_ylim(-1.5, 1.5)
                  ax.set_xlabel(L"$x$")
                  ax.set_title("Graph of trigonometric functions")
                  ax.legend()
  
                  # The second one when the axes are arranged in three rows and two columns
                  ax = fig.add_subplot(3,2,2)
                  ax.plot(x3, sinh.(x3), label = L"$\sinh(x)$")
                  ax.plot(x3, cosh.(x3), label = L"$\cosh(x)$")
                  ax.plot(x3, tanh.(x3), label = L"$\tanh(x)$")
                  ax.set_xlabel(L"$x$")
                  ax.set_title("Graph of hyperbolic functions")
                  ax.legend()
  
                  # The third one when the axes are arranged in three rows and two columns
                  ax = fig.add_subplot(3,2,3)
                  ax.plot(x1, 1 ./ sin.(x1), label = L"$\csc(x)$")
                  ax.plot(x1, 1 ./ cos.(x1), label = L"$\sec(x)$")
                  ax.plot(x1, 1 ./ tan.(x1), label = L"$\cot(x)$")
                  ax.set_ylim(-10, 10)
                  ax.set_xlabel(L"$x$")
                  ax.set_title("Graph of the reciprocal of trigonometric functions")
                  ax.legend()
  
                  # The fourth one when the axes are arranged in three rows and two columns
                  ax = fig.add_subplot(3,2,4)
                  ax.plot(x3, 1 ./ sinh.(x3), label = L"$\mathrm{csch}(x)$")
                  ax.plot(x3, 1 ./ cosh.(x3), label = L"$\mathrm{sech}(x)$")
                  ax.plot(x3, 1 ./ tanh.(x3), label = L"$\coth(x)$")
                  ax.set_ylim(-4, 4)
                  ax.set_xlabel(L"$x$")
                  ax.set_title("Graph of the reciprocal of hyperbolic functions")
                  ax.legend()
  
                  # The fifth one when the axes are arranged in three rows and two columns
                  ax = fig.add_subplot(3,2,5)
                  ax.plot(x2, asin.(x2), label = L"$\sin^{-1}(x)$")
                  ax.plot(x2, acos.(x2), label = L"$\cos^{-1}(x)$")
                  ax.plot(x3, atan.(x3), label = L"$\tan^{-1}(x)$")
                  ax.set_xlabel(L"$x$")
                  ax.set_title("Graph of inverse trigonometric functions")
                  ax.legend()
  
                  # The sixth one when the axes are arranged in three rows and two columns
                  ax = fig.add_subplot(3,2,6)
                  ax.plot(x3, asinh.(x3), label = L"$\sinh^{-1}(x)$")
                  ax.plot(x4, acosh.(x4), label = L"$\cosh^{-1}(x)$")
                  ax.plot(x2, atanh.(x2), label = L"$\tanh^{-1}(x)$")
                  ax.set_xlabel(L"$x$")
                  ax.set_title("Graph of inverse hyperbolic functions")
                  ax.legend()
  
                  # Adjust axis spacing with subplots_adjust
                  # wspace for horizontal, hspace for vertical
                  subplots_adjust(wspace=0.2, hspace=0.3)
  
                  show()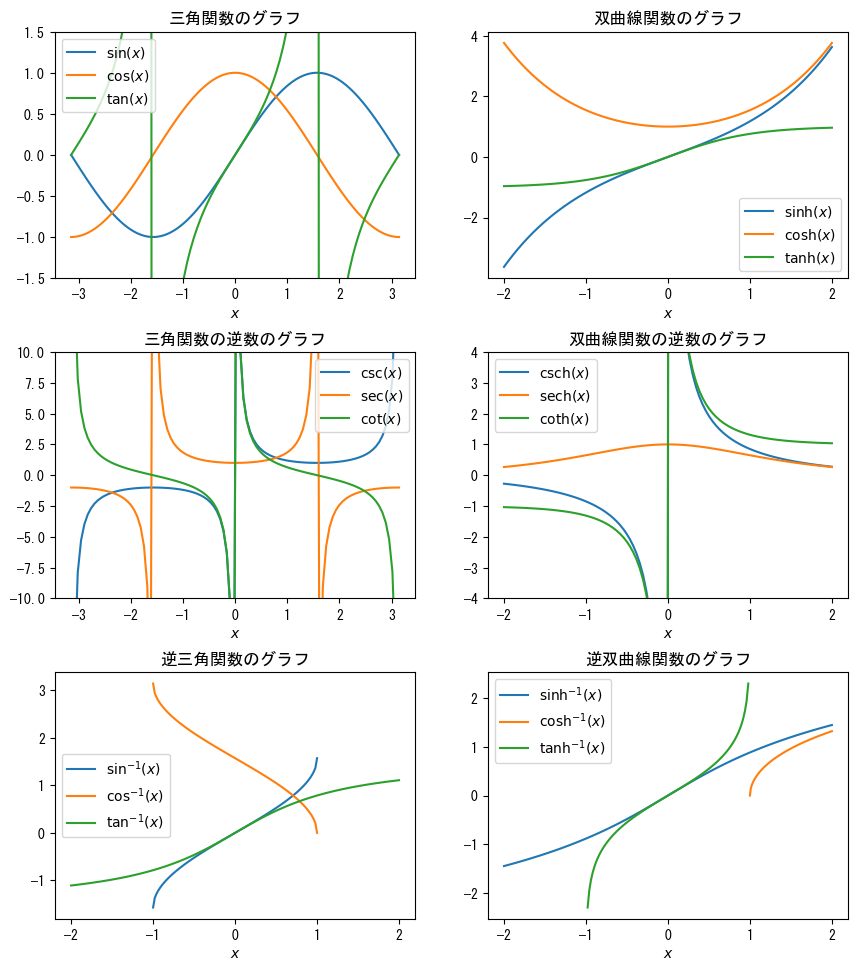
                

  

Logarithmic Scale Graphs

• single-logarichmic graph

                  fig = figure() 
                  x = collect(range(0, 5, length = 5))
  
                  ax = fig.add_subplot(1,1,1)
  
                  # ax.set_yscale("log") creates a semi-logarithmic graph (y-axis is logarithmic scale)
                  ax.set_yscale("log")
  
                  ax.plot(x, 5 * exp.(- 2 * x), marker = "o")
                  ax.set_title("In a semi-logarithmic graph, exponential functions appear as straight lines")
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$5e^{-2x}$")
  
                  show()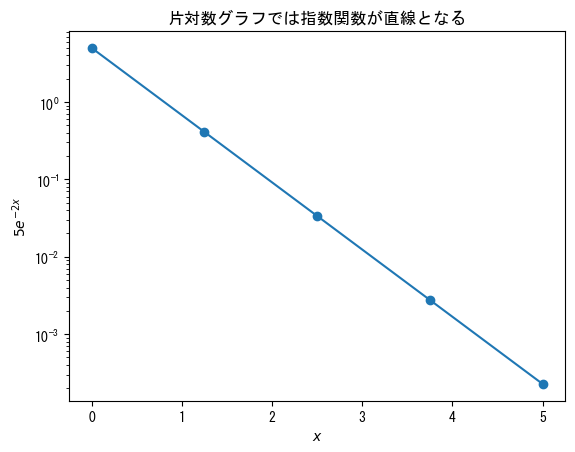
                

  

• double-logarithmic graph

                  fig = figure() 
                  x = collect(range(1, 100, length = 10))
  
                  ax = fig.add_subplot(1,1,1)
  
                  # Add ax.set_xscale("log") to create a double logarithmic graph (logarithmic scale on both the x-axis and y-axis)
                  ax.set_xscale("log")
                  ax.set_yscale("log")
  
                  ax.plot(x, 10 * x .^ (- 5 / 3), marker = "o")
                  ax.set_title("In a logarithmic graph, power functions become straight lines")
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$10x^{-5/3}$")
  
                  show()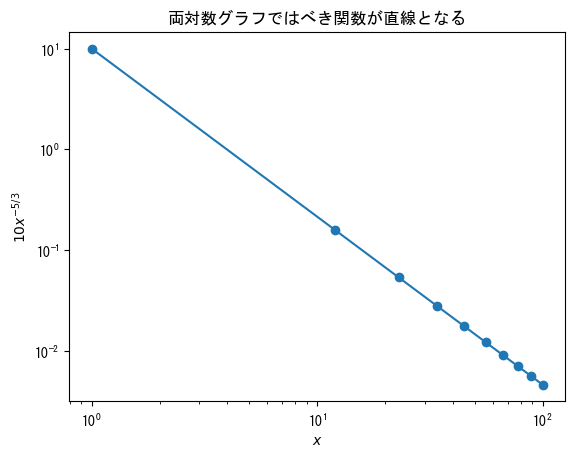
                

  

• When using ticks (setting axis values) in a logarithmic graph, it is best to use them in conjunction with ticklabels (or else the graph may not display well).

                  # On logarithmic scale graphs, minor ticks are basically displayed as they are
                  # If you want to delete it, add the following description
                  rc("ytick.minor", size = 0) # When the x-axis is on a logarithmic scale, use xtick.minor
  
                  fig = figure() 
                  x = collect(range(0, 5, length = 5))
  
                  ax = fig.add_subplot(1,1,1)
  
                  ax.set_yscale("log")
  
                  # Set the vector of values you want to set on the y-axis
                  vector_y = [0.02; 0.7; 1.4; 5]
                  ax.set_yticks(vector_y)
                  ax.set_yticklabels(string.(vector_y))
  
                  ax.plot(x, 5 * exp.(- 2 * x), marker = "o")
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$5e^{-2x}$")
  
                  show()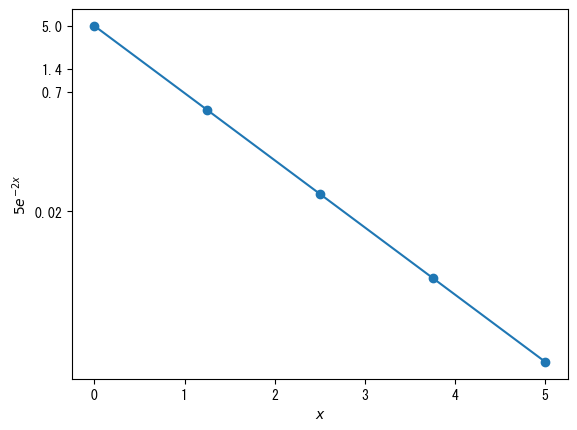
                

  

Histogram

• Basic Histogram

                  using Random
                  using Dates
                  rng = MersenneTwister(Millisecond(now()).value)
  
                  fig = figure() 
                  x = [randn(rng, 1000); 2.0 * randn(rng, 1000) .+ 5]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # ax.hist(vector) produces a histogram
                  ax.hist(x)
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel("histogram")
  
                  show()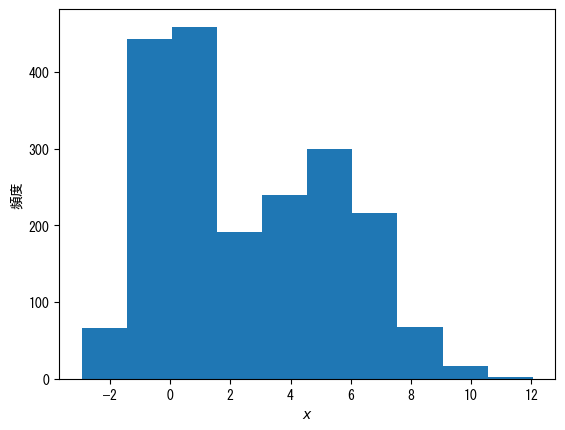
                

  

• change the grade number

                  using Random
                  using Dates
                  rng = MersenneTwister(Millisecond(now()).value)
  
                  fig = figure() 
                  x = [randn(rng, 1000); 2.0 * randn(rng, 1000) .+ 5]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # Specify the number of classes with the bins option
                  ax.hist(x, bins = 20)
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel("histogram")
  
                  show()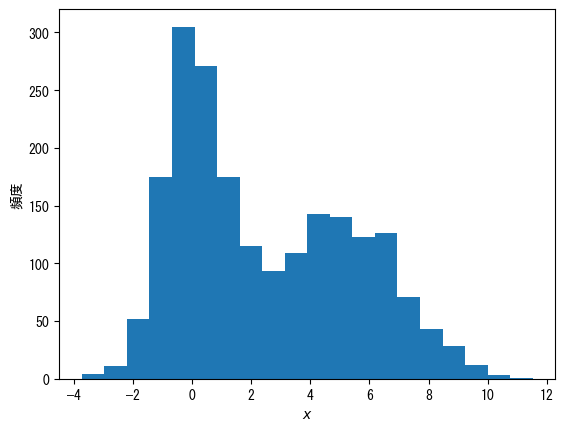
                

  

• Make it a probability distribution, not a frequency

                  using Random
                  using Dates
                  rng = MersenneTwister(Millisecond(now()).value)
  
                  fig = figure() 
                  x = [randn(rng, 1000); 2.0 * randn(rng, 1000) .+ 5]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # When density = true, it becomes a probability distribution rather than a frequency distribution
                  ax.hist(x, bins = 20, density = true)
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$p(x)$")
  
                  show()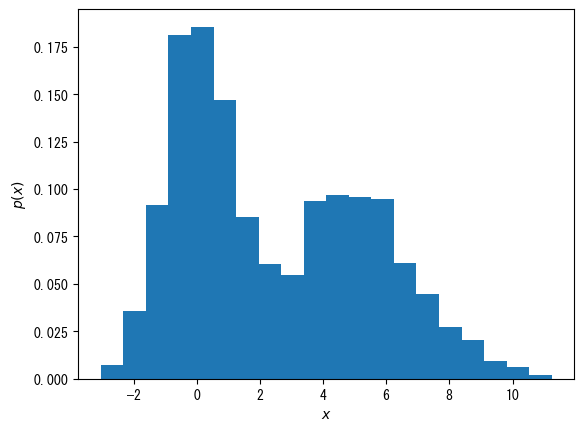
                

  

• Bars only on the outer border (useful for displaying multiple histograms)

                  using Random
                  using Dates
                  rng = MersenneTwister(Millisecond(now()).value)
  
                  fig = figure() 
                  x1 = randn(rng, 1000)
                  x2 = 2.0 * randn(rng, 1000) .+ 5
                  x3 = [x1; x2]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # When histtype = "step", only the outer frame is displayed
                  ax.hist(x1, bins = 20, density = true, histtype = "step", label = L"$p_1(x)$")
                  ax.hist(x2, bins = 20, density = true, histtype = "step", label = L"$p_2(x)$")
                  ax.hist(x3, bins = 20, density = true, histtype = "step", label = L"$p_{1 + 2}(x)$")
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$p(x)$")
                  ax.legend()
  
                  show()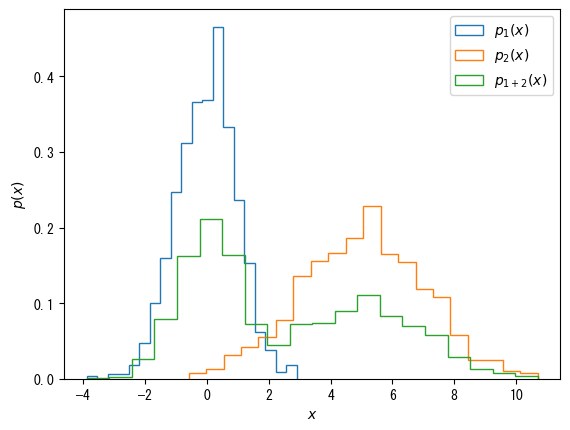
                

  

• A note on histograms

  If you want to plot something more advanced, such as a histogram of a line chart, you have to get a vector of the histogram, which can be obtained by the fit function in StatsBase, but it is quite tedious (this is where Python ( numpy) wins hands down).

Point color and point size in scatter plots by scatter

• Specify a different vector for the color of a point in a scatterplot with scatter

                  fig = figure() 
                  height = [172.3; 165; 179.6; 174.5; 173.8; 165.4; 164.5; 174.9; 166.8; 185]
                  mass = [75.24; 55.8; 78; 71.1; 67.7; 55.4; 63.7; 77.2; 67.5; 84.6]
                  fat = [21.3; 15.7; 20.1; 18.4; 17.1; 22; 32.2; 36.9; 27.6; 14.4]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # By specifying a vector with the c option, the points will be colored according to the values in that vector
                  ax.scatter(height, mass, c = fat)
  
                  ax.set_xlabel("height [cm]")
                  ax.set_ylabel("weight [kg]")
  
                  show()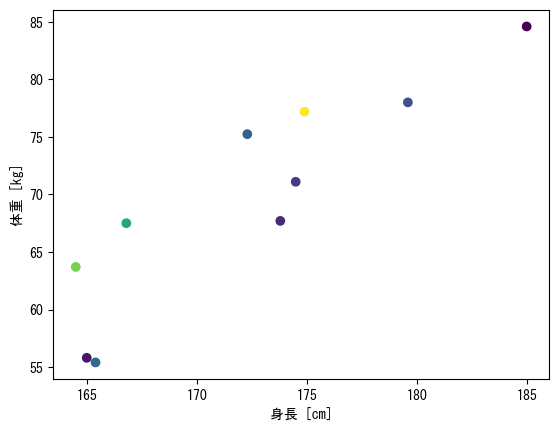
                

  

• Display a color bar that maps colors to numerical values

                  fig = figure() 
                  height = [172.3; 165; 179.6; 174.5; 173.8; 165.4; 164.5; 174.9; 166.8; 185]
                  mass = [75.24; 55.8; 78; 71.1; 67.7; 55.4; 63.7; 77.2; 67.5; 84.6]
                  fat = [21.3; 15.7; 20.1; 18.4; 17.1; 22; 32.2; 36.9; 27.6; 14.4]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # Assign the scatter plot itself as a variable (in this case, the variable c_points)
                  c_points = ax.scatter(height, mass, c = fat)
  
                  # colorbar(c_points, ax = ax) adds a color bar
                  colorbar(c_points, ax = ax)
  
                  ax.set_xlabel("height [cm]")
                  ax.set_ylabel("weight [kg]")
  
                  show()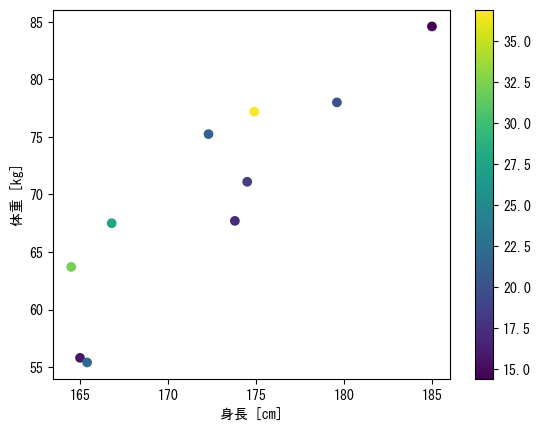
                

  

• Option 1 for color, color bar

                  fig = figure() 
                  height = [172.3; 165; 179.6; 174.5; 173.8; 165.4; 164.5; 174.9; 166.8; 185]
                  mass = [75.24; 55.8; 78; 71.1; 67.7; 55.4; 63.7; 77.2; 67.5; 84.6]
                  fat = [21.3; 15.7; 20.1; 18.4; 17.1; 22; 32.2; 36.9; 27.6; 14.4]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # The vmax and vmin options allow you to set the maximum and minimum values for colors
                  c_points = ax.scatter(height, mass, c = fat, vmin = 10, vmax = 40)
  
                  # Color bars are named with the label option
                  colorbar(c_points, ax = ax, label = "body fat [%]")
  
                  ax.set_xlabel("height [cm]")
                  ax.set_ylabel("weight [kg]")
  
                  show()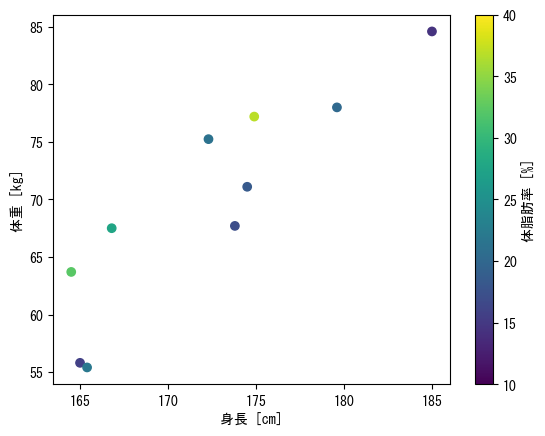
                

  

• Option 2 for color, color bar

                  fig = figure() 
                  height = [172.3; 165; 179.6; 174.5; 173.8; 165.4; 164.5; 174.9; 166.8; 185]
                  mass = [75.24; 55.8; 78; 71.1; 67.7; 55.4; 63.7; 77.2; 67.5; 84.6]
                  fat = [21.3; 15.7; 20.1; 18.4; 17.1; 22; 32.2; 36.9; 27.6; 14.4]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # Colors can be changed with the cmap option
                  # viridis : Default blue→yellow
                  # jet : rainbow colors
                  # hsv : periodic rainbow colors
                  c_points = ax.scatter(height, mass, c = fat, cmap = get_cmap(:hsv))
  
                  # The value set in the ticks option is displayed
                  # Furthermore, assign the color bar itself to another variable (in this case, cbar), and use cbar.ax.set_yticklabels to change the display
                  cbar = colorbar(c_points, ax = ax, label = "body fat [%]", ticks = [15; 25; 35])
                  cbar.ax.set_yticklabels(["low"; "mid"; "high"])
  
                  ax.set_xlabel("height [cm]")
                  ax.set_ylabel("weight [kg]")
  
                  show()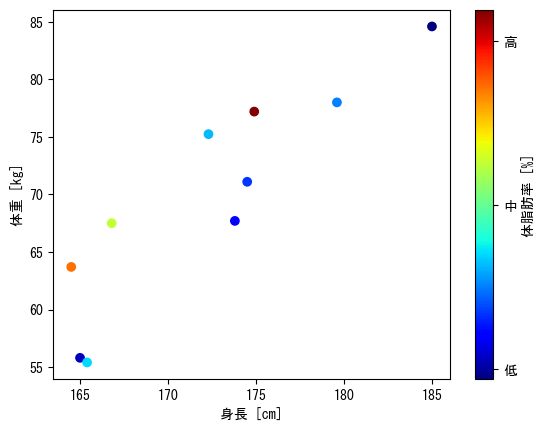
                

  

• Dot size

                  fig = figure() 
                  height = [172.3; 165; 179.6; 174.5; 173.8; 165.4; 164.5; 174.9; 166.8; 185]
                  mass = [75.24; 55.8; 78; 71.1; 67.7; 55.4; 63.7; 77.2; 67.5; 84.6]
                  fat = [21.3; 15.7; 20.1; 18.4; 17.1; 22; 32.2; 36.9; 27.6; 14.4]
                  age = [27; 25; 31; 32; 28; 36; 42; 33; 54; 28]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # You can choose the size of the dots as an option
                  # (markersize for plots)
                  # However, in the case of scatter, you can change the size of each point by specifying a vector in c
                  c_points = ax.scatter(height, mass, c = fat, s = age * 4)
  
                  cbar = colorbar(c_points, ax = ax, label = "body fat [%]", ticks = [15; 25; 35])
                  cbar.ax.set_yticklabels(["low"; "mid"; "high"])
  
                  ax.set_xlabel("height [cm]")
                  ax.set_ylabel("weight [kg]")
                  ax.set_title("Marker size corresponds to age")
  
                  show()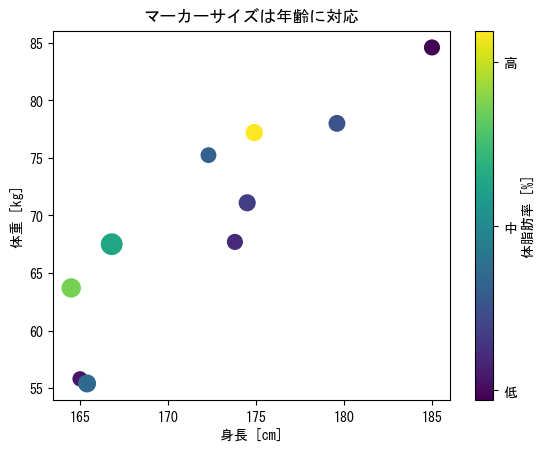
                

  

Heatmap using imshow, pcolor

• imshow is like displaying a matrix as you see it

                  fig = figure() 
  
                  matrix = [2 3 0 0;
                       1 2 3 0;
                       0 1 2 3;]
  
                  ax = fig.add_subplot(1,1,1)
  
                  # min, vmax, and cmap options can also be used (see scatter)
                  c_matrix = ax.imshow(matrix)
  
                  # Color bars can also be used
                  # label and ticks options are also available
                  colorbar(c_matrix, ax = ax, label = "matrix value")
  
                  ax.set_xlabel("column")
                  ax.set_ylabel("row")
  
                  show()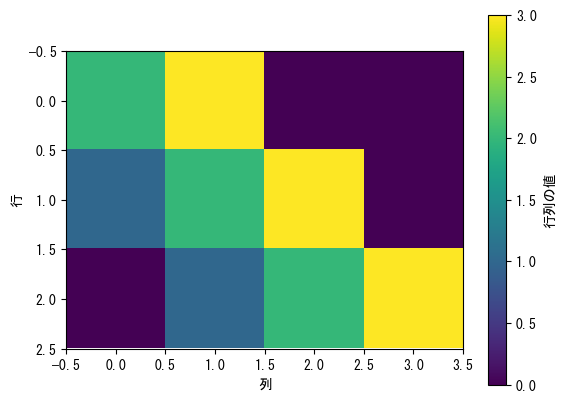
                

  

• If the height of the color bar is uncomfortable

                  fig = figure() 
  
                  matrix = [2 3 0 0;
                       1 2 3 0;
                       0 1 2 3;]
  
                  ax = fig.add_subplot(1,1,1)
  
                  c_matrix = ax.imshow(matrix)
  
                  # The quickest way is to set fraction = (row size) / (column size) * 0.046 and pad = 0.04.
                  colorbar(c_matrix, ax = ax, label = "matrix value", fraction = 3 / 4 * 0.046, pad = 0.04)
  
                  ax.set_xlabel("column")
                  ax.set_ylabel("row")
  
                  show()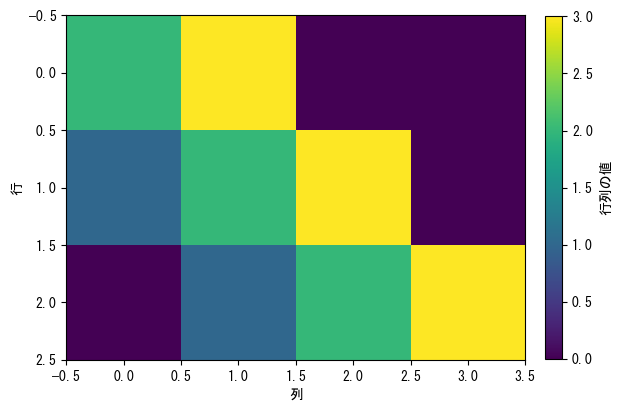
                

  

• pcolor is an image like contour lines, where x and y coordinates can be specified
  However, if nothing is specified, the line direction of the matrix will be x and the columns will be y direction (opposite to imshow)

                  fig = figure() 
  
                  # Create a vector for the values of x and y
                  x = collect(range(- 2pi, 2pi, length = 100))
                  y = collect(range(- pi, pi, length = 100))
  
                  # Set y as the vector (horizontal vector)
                  y = transpose(y)
  
                  # Convert x and y into a matrix
                  x, y = x .+ 0 * y, 0 * x .+ y
  
                  ax = fig.add_subplot(1,1,1)
  
                  # The basic format is ax.pcolor(matrix specifying x coordinates, matrix specifying y coordinates, matrix for heat map, shading = "auto")
                  # The vmin, vmax, and cmap options can also be used (see scatter)
                  c_pcolor = ax.pcolor(x, y, sin.(x .+ y), shading = "auto")
  
                  # Color bars can also be used
                  # label and ticks options are also available
                  colorbar(c_pcolor, ax = ax, label = L"$\sin(x+y)$")
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$y$")
                  ax.set_xticks([-2pi; -pi; 0; pi; 2pi])
                  ax.set_xticklabels([L"$-2\pi$"; L"$-\pi$"; L"$0$"; L"$\pi$"; L"$2\pi$"])
                  ax.set_yticks([-pi; 0; pi])
                  ax.set_yticklabels([L"$-\pi$"; L"$0$"; L"$\pi$"])
  
                  show()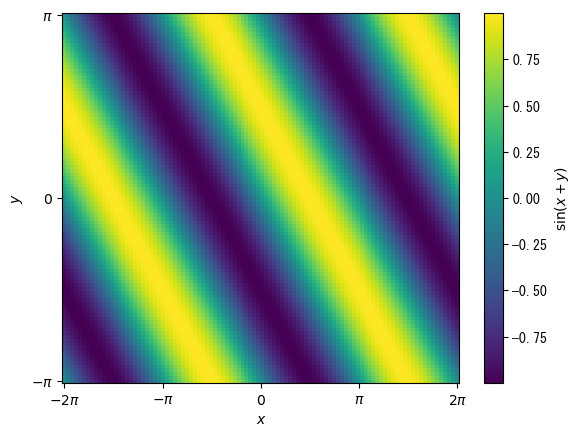
                

  

3D Graph

• Basics of 3D Graphs

                  # 3D graphs are basically convenient because you can freely change the viewpoint using the mouse
                  # To make this possible, it is necessary to draw the graph in a separate window
                  # If you set pygui(true), the graph will open in a separate window
                  # Conversely, if you set pygui to false, the graph will be displayed on the Jupyter notebook
                  pygui(true)
  
                  fig = figure() 
                  t = collect(range(0, 2pi, length = 100))
                  x = sin.(t)
                  y = cos.(t)
                  z = t + sin.(2t)
  
                  # Adding "3d" to projection makes it a 3D graph
                  ax = fig.add_subplot(1,1,1, projection = "3d")
  
                  # A plot is a 3D line graph that also requires a vector for the z-coordinate
                  ax.plot(x, y, z)
  
                  # ax.set_zlabel, ax.set_zticks, ax.set_zticklabels, and ax.set_zlim can also be used
                  ax.set_xlabel(L"$x = \sin(t)$")
                  ax.set_ylabel(L"$y = \cos(t)$")
                  ax.set_zlabel(L"$z = t + \sin(2t)$")
  
                  show()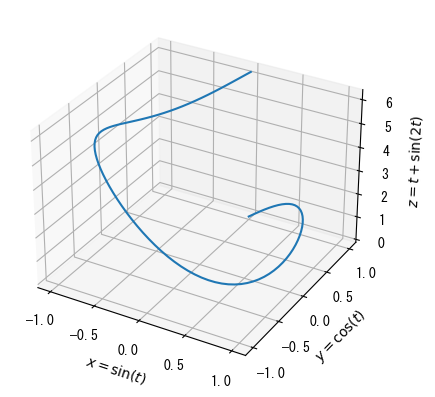
                

  

• Dispersal Chart

                  pygui(true)
  
                  fig = figure() 
                  age = [27; 25; 31; 32; 28; 36; 42; 33; 54; 28]
                  height = [172.3; 165; 179.6; 174.5; 173.8; 165.4; 164.5; 174.9; 166.8; 185]
                  mass = [75.24; 55.8; 78; 71.1; 67.7; 55.4; 63.7; 77.2; 67.5; 84.6]
                  fat = [21.3; 15.7; 20.1; 18.4; 17.1; 22; 32.2; 36.9; 27.6; 14.4]
  
                  ax = fig.add_subplot(1,1,1, projection = "3d")
  
                  # 3D scatter can specify vectors corresponding to colors in the same way as 2D scatter
                  c_points = ax.scatter(height, mass, fat, c = age)
  
                  # The color bars are close to the graph when set to default, so it is better to move them away a little using the pad option
                  colorbar(c_points, ax = ax, label = "age", pad = 0.15)
  
                  ax.set_xlabel("height [cm]")
                  ax.set_ylabel("weight [kg]")
                  ax.set_zlabel("body fat [%]")
  
                  show()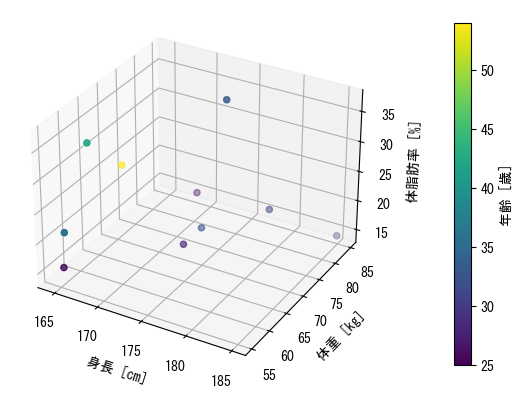
                

  

• Curved surface (wireframe): alternative to pcolor

                  pygui(true)
  
                  fig = figure() 
  
                  x = collect(range(- 2pi, 2pi, length = 100))
                  y = collect(range(- pi, pi, length = 100))
  
                  y = transpose(y)
  
                  x, y = x .+ 0 * y, 0 * x .+ y
  
                  ax = fig.add_subplot(1,1,1, projection = "3d")
  
                  # Displaying curved surfaces with ax.plot_wireframe
                  ax.plot_wireframe(x, y, sin.(x) + cos.(y))
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$y$")
                  ax.set_zlabel(L"$\sin(x)+\cos(y)$")
  
                  ax.set_xticks([-2pi; -pi; 0; pi; 2pi])
                  ax.set_xticklabels([L"$-2\pi$"; L"$-\pi$"; L"$0$"; L"$\pi$"; L"$2\pi$"])
                  ax.set_yticks([-pi; 0; pi])
                  ax.set_yticklabels([L"$-\pi$"; L"$0$"; L"$\pi$"])
  
                  show()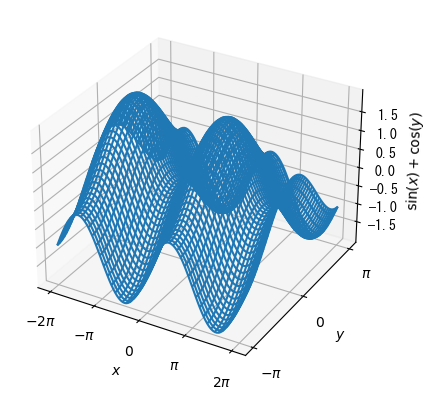
                

  

• colored surface

                  pygui(true)
  
                  fig = figure() 
  
                  x = collect(range(- 2pi, 2pi, length = 100))
                  y = collect(range(- pi, pi, length = 100))
  
                  y = transpose(y)
  
                  x, y = x .+ 0 * y, 0 * x .+ y
  
                  ax = fig.add_subplot(1,1,1, projection = "3d")
  
                  # Color-coded surface display with ax.plot_surface with cmap option
                  c_surface = ax.plot_surface(x, y, sin.(x) + cos.(y), cmap = get_cmap(:viridis))
  
                  colorbar(c_surface, ax = ax, pad = 0.15)
  
                  ax.set_xlabel(L"$x$")
                  ax.set_ylabel(L"$y$")
                  ax.set_zlabel(L"$\sin(x)+\cos(y)$")
  
                  ax.set_xticks([-2pi; -pi; 0; pi; 2pi])
                  ax.set_xticklabels([L"$-2\pi$"; L"$-\pi$"; L"$0$"; L"$\pi$"; L"$2\pi$"])
                  ax.set_yticks([-pi; 0; pi])
                  ax.set_yticklabels([L"$-\pi$"; L"$0$"; L"$\pi$"])
  
                  show()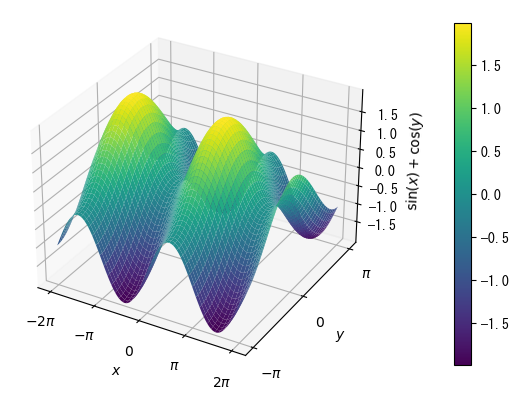
                

  

Animation

• The animation is created in the manner of a so-called flipbook.
  That is, the graph is displayed for a certain (short) amount of time, and the action is repeated.
  In the case of PyPlot, the graph is repeatedly erased and then displayed.

                  # Animations are displayed in a separate window, similar to 3D graphs
                  # Incidentally, saving animations in PyPlot is troublesome, so it is better to give up on that
                  pygui(true)
  
                  using Printf
  
                  fig = figure()
                  ax = fig.add_subplot(1,1,1)
  
                  q = pi / 4
                  v0 = 5.0
                  v0x = v0 * cos(q)
                  v0y = v0 * sin(q)
                  g = 9.8
  
                  t = [0.0]
                  x = [0.0]
                  y = [0.0]
  
                  # For loop to display animation
                  for it = 1:200
  
                      t_now = it * 0.0035
                      x_now = v0x * t_now
                      y_now = v0y * t_now - 0.5 * g * t_now ^ 2
                              
                      t = [t; t_now]
                      x = [x; x_now]
                      y = [y; y_now]
                              
                      # Graph drawing
                              
                      # Delete the previous graph
                      ax.cla()
                              
                      # Plotting a new graph
                      ax.scatter(x_now, y_now)
                      ax.plot(x,y)
                              
                      ax.set_xlabel("horizontal distance [m]")
                      ax.set_ylabel("vertical distance [m]")
                              
                      # It is better to decide the maximum and minimum values for the axis in advance
                      ax.set_xlim(0, 3)
                      ax.set_ylim(0, 0.8)
                              
                      ax.set_title("t = " * @sprintf("%5.3f", t_now) * " [sec]")
  
                      # Draw a graph and wait for the time (seconds) specified in ()
                      pause(0.05)
  
                  end