交通流の離散モデル（4-4）

ナーゲルとシュレンケンベルクの標準模型４

つぎに確率減速 R がゼロでない場合を見てみる。

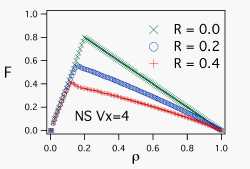
右に U = 4 の場合で、R を 0.0、0.2、0.4 と変えてみた結果を示す。 R = 0 と比較して有限 R の一番の特徴は渋滞の起こりの早さと、渋滞が起こった後のＦの値の減少である。 渋滞が起こる前のρの小さな領域ではこれまでと余り変化がなく、ρが０に近づくときの振る舞いは前と同じ

で与えられる「自由交通」であるが、ρの大きい領域での振舞いが異なる。具体的にはρが１に近づくにつれて

という振舞いにだんだんなっていく。ちなみにこのように極限である振舞いに近づくことを「漸近的に一致する」と呼ぶ。

渋滞領域での流束は、グラフを仔細に見ると、実際は直線ではなく上に凸な曲線で、密度を下げて行った自由交通との境目の領域付近では、流束は(4.8)よりもかなり小さくなっている。

こうしてわかる事は、０でない値を持つ R は、その値が小さくても、臨界密度を引き下げ、渋滞での流束を割と大きく減らす、と言う事である。

確率減速 R は道路の状況にもよるが、また運転者の技量や「注意深さ」にもよるであろう。国ごと地方ごとに運転の習慣が異なることは、知らない土地で運転するとすぐ気づくことである。ここで得た交通基本図から示唆されるのは、小さい R の値で表される注意深い運転習慣をもつ土地の方が、大きい R で表される荒っぽい運転者の多い土地より渋滞発生の臨界密度が高く、渋滞が起こってもその程度が小さい。しかし渋滞が起こるまではどちらでもあまり変わらない。考えてみればこれは当然の事であるが、車の多い大都市の方が運転マナーが一般によくなるという経験的事実とも合致する。